이번에는 다음에 리뷰할 DETR 논문에 등장하는 Bipartite Matching에 대해서 알아보도록 하겠습니다.
Bipartite Matching은 그래프 이론과 조합 최적화에서 중요한 개념입니다.
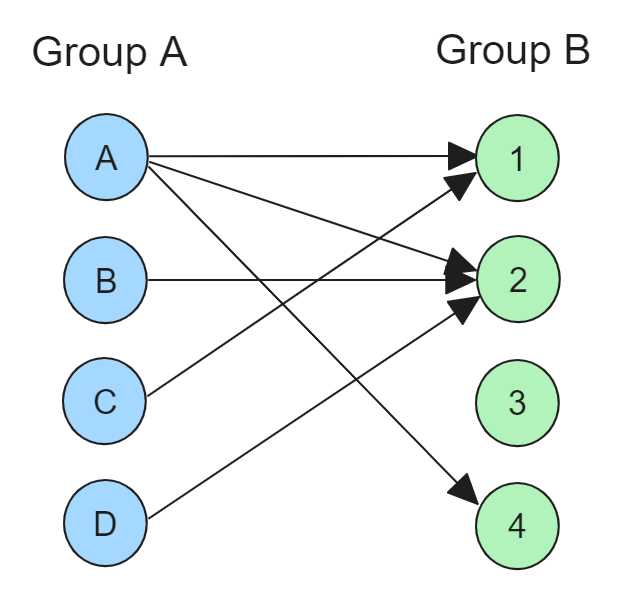
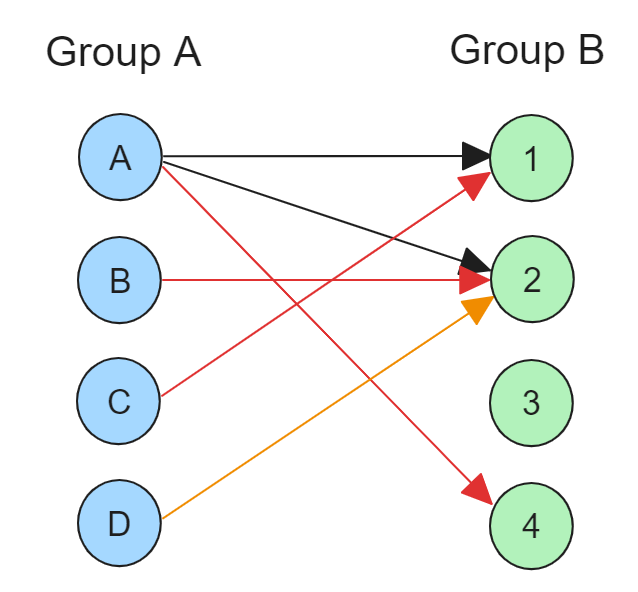
이렇게 Group A, Group B 두 집단이 있을 때, 모든 간선의 용량이 1이면서 양쪽 노드가 서로 다른 집단에 속하는 그래프를 이분 그래프(Bipartite Graph)라고 합니다.
Bipartie Macthing은 bipartite graph에서 maximum matching(최대 매칭)을 찾는 문제입니다.
최대 매칭을 찾는 것은 두 그룹 사이의 일대일 관계를 설정하는 것을 의미하는데, 가능한 한 많은 노드 쌍이 한 연결로 매칭되는 경우를 나타냅니다.
각 노드는 다른 그룹의 한 노드에 대해서만 매칭이 가능합니다.
알고리즘
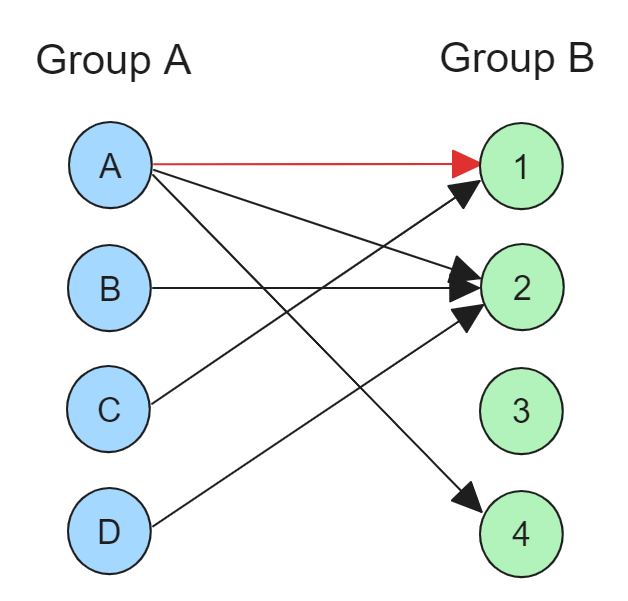
우선 노드 A는 노드 1을 매칭할 수 있습니다. (총 매칭 수: 1)
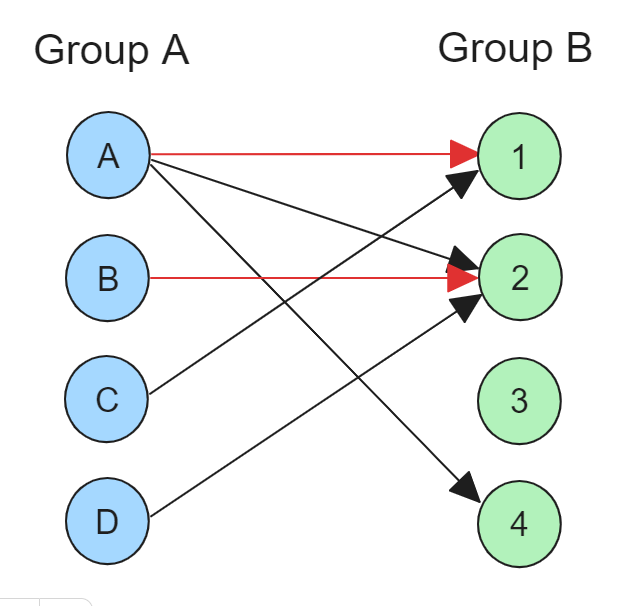
그 다음 노드 B는 노드 2와 매칭할 수 있습니다. (총 매칭 수: 2)
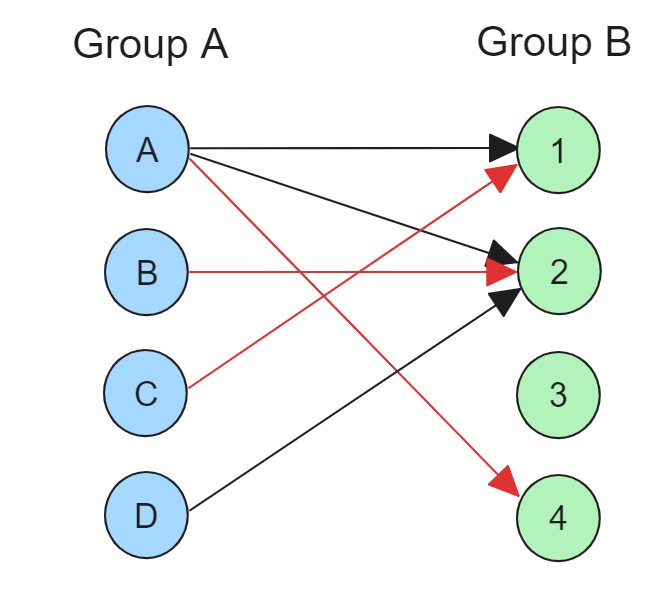
노드 C는 노드 1과 매칭하려고 하는데, 노드 1은 이미 노드 A와 매칭되어 있습니다. 따라서 노드 A는 다른 노드와 매칭하기 위해 경로를 다시 찾습니다. 노드 2는 이미 노드 B와 매칭되어 있고, 노드 B는 유일하게 노드 2와 연결되어 있습니다. 결국 노드 A는 노드 4와 매칭이 됩니다. (총 매칭 수: 3)
노드 D는 노드 2와 매칭하려고 합니다. 그러나 노드 2는 이미 노드 B와 연결되어 있기 때문에 매칭할 수 없습니다. 노드 D가 노드 2를 매칭하면 다시 노드 B는 다시 매칭할 노드를 찾을 것이므로 계속해서 반복되기 때문에 매칭이 불가능합니다.
따라서 총 매칭 수는 3이 됩니다.
객체 탐지에서 Bipartite Matching은 예측된 바운딩 박스와 실제 대상 바운드 박스를 매칭하는 데 사용됩니다. 각 예측된 바운딩 박스를 한 개의 대상 바운드 박스와 일치시키는 것이 목표입니다. 최적화 알고리즘 중 하나인 헝가리 알고리즘(Hungarian Algorithm)은 예측된 객체와 실제 객체 사이의 최적 일치를 찾는 데 사용되는 알고리즘입니다.
가능한 모든 매칭(예측된 객체와 실제 객체 간의 가능한 연결)에 대해 가중치를 할당합니다. 이 가중치는 두 객체 사이의 관계를 나타내며, 두 객체 간의 관련성이 높을수록 가중치는 낮아집니다. 그런 다음 알고리즘은 이러한 가중치를 최소화하도록 하여 최적의 매칭을 찾습니다.
이러한 방식으로 각 예측된 객체를 가장 적합한 실제 객체와 매치시키는 최상의 조합을 찾아냅니다. 이것은 객체 탐지에서 예측된 객체 박스와 실제 객체 박스 사이의 관계를 설정하고, 어떤 예측이 어떤 실제 객체와 일치하는지를 결정하는 데 사용됩니다.